분할 정복 알고리즘

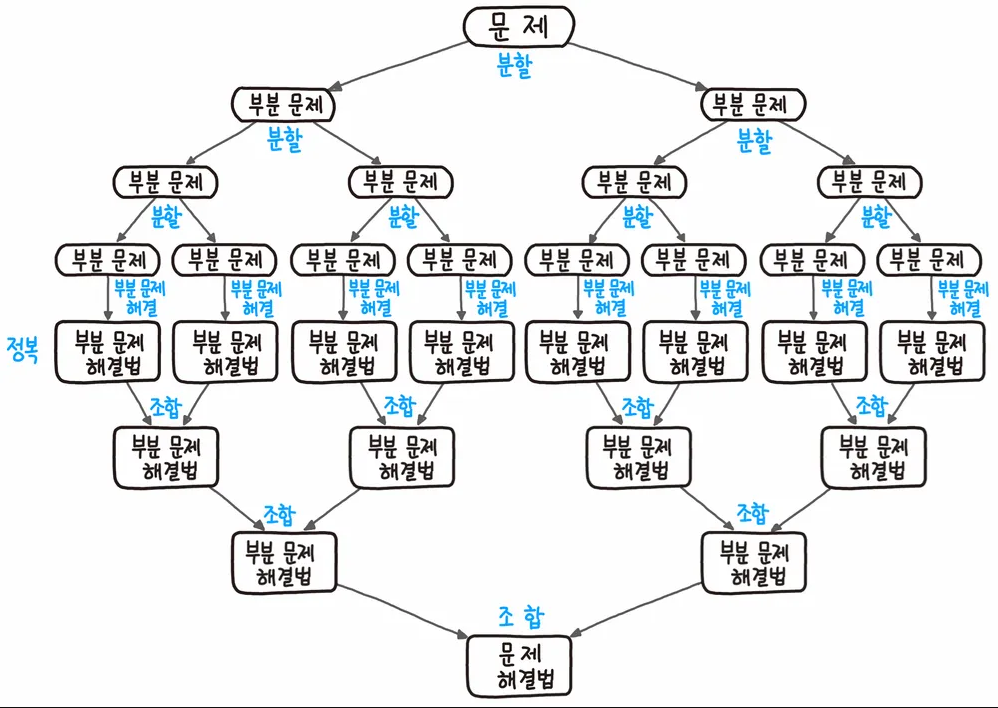분할 정복 알고리즘(Divide and conquer)은 문제를 반씩 나누어 해결하고, 하위 문제에 대한 결과를 원래 문제에 대한 결과로 조합해 해결하는 알고리즘이다.

특징

1. 문제를 두 개 이상의 작은 문제로 나눈다.
2. 각각의 작은 문제를 재귀적으로 해결한다
3. 해결한 결과를 병합하여 최종 답을 얻는다.

예시

병합 정렬

#include <iostream>
#include <vector>
using namespace std;

// 두 개의 정렬된 부분 배열을 병합하는 함수
void merge(vector<int>& arr, int left, int mid, int right) {
    vector<int> temp; // 병합 결과를 저장할 임시 배열
    int leftIndex = left, rightIndex = mid + 1;

    // 두 부분 배열을 비교하며 병합
    while (leftIndex <= mid && rightIndex <= right) {
        if (arr[leftIndex] < arr[rightIndex]) {
            temp.push_back(arr[leftIndex++]);
        } else {
            temp.push_back(arr[rightIndex++]);
        }
    }

    // 왼쪽 부분 배열에 남은 요소 추가
    while (leftIndex <= mid) temp.push_back(arr[leftIndex++]);

    // 오른쪽 부분 배열에 남은 요소 추가
    while (rightIndex <= right) temp.push_back(arr[rightIndex++]);

    // 원래 배열에 병합된 결과 복사
    for (int i = 0; i < temp.size(); i++) {
        arr[left + i] = temp[i];
    }
}

// 병합 정렬 함수 (재귀적으로 배열을 나누고 병합)
void mergeSort(vector<int>& arr, int left, int right) {
    if (left >= right) return; // 기저 조건: 배열 크기가 1이면 종료

    int mid = left + (right - left) / 2; // 중간 지점 계산
    mergeSort(arr, left, mid);    // 왼쪽 부분 정렬
    mergeSort(arr, mid + 1, right); // 오른쪽 부분 정렬
    merge(arr, left, mid, right); // 정렬된 두 부분 병합
}

int main() {
    vector<int> arr = {5, 2, 9, 1, 5, 6};

    mergeSort(arr, 0, arr.size() - 1); // 병합 정렬 실행

    // 정렬된 배열 출력
    for (int num : arr) {
        cout << num << " ";
    }
}

거듭제곱 계산

long long power(long long base, long long exp) {
    if (exp == 0) return 1;
    long long half = power(base, exp / 2);
    return (exp % 2 == 0) ? half * half : half * half * base;
}

예를 들어 2^10을 계산할 때는 일반적으로 시작복잡도가 O(n)인 반복문을 사용한다. 하지만 분할 정복을 활용한 거듭제곱은 시간복잡도가 O(log n)으로 더 빠르게 계산할 수 있다.

공식 : x^n = (n%2==0)? (x^(n/2))^2 : x*(x^((n-1)/2))^2

n을 절반으로 줄여서 재귀적으로 해결할 수 있다.

Meet in the middle?

Meet in the middle 기법은 분할 정복 알고리즘처럼 문제를 반으로 나누지만 하위 문제를 계속 나누는 것이 아닌 두 개의 문제로 나누는 차이가 있다. 완전 탐색으로 풀기 어려운 문제를 해결할 때 사용되며, 시간 복잡도를 O(2^(N/2)) 수준으로 줄이는 것이 목표다.

• 관련 알고리즘 문제
• 해답